Could We Blow Up a Star?
In my debut science fiction thriller Prometheus Blue in the year 2025 the world learns that a Sun-sized star fragment, 6 light-years distant, is heading directly for our Sun at 2,574 kilometers a second. It will destroy the Solar System and all the inner planets in 700 years. The first of a planned 6 book series called the Third Stone series, Prometheus Blue examines Humanity’s initial response to this devastating news.
I mentioned in my last post that this is not a hero-saves-the-planet story. Far from it. The heart of the story depends on convincing my readers that this event is a true planet killer — that Earth’s destruction is a certainty and cannot be avoided. Nothing can stop this nuclear engine of destruction, named Blake’s Fragment in honor of its first observer. Blake’s is simply too big, too massive, too hot, too fast. Some might think our vast store of nuclear weapons can destroy or divert it. Not a chance. It would be like reversing Niagara Falls with a squirt gun: pathetically too little force and it’s all made of the same stuff anyway.
So no. No hero is going to figure out a way to blow this thing up or to divert it somewhere else.
Because you see, if we believe this could still be a hero story, that would change everything. That story’s been done. You’ve seen the asteroid movies, maybe read a couple of the books (like Arthur C. Clarke’s Hammer of God). Ultimately Earth wins. OK in some cases, Earth loses – usually to aliens or plague or zombies – but we’ve only got a few months to think about it. So no, for the story Prometheus story to work, the reader has to know that planet Earth’s salvation is not an option. I have to prove it to you. And that’s exactly what I do in Prometheus Blue. But while I endeavor to explain these concepts clearly, I don’t go deep into the math. That might be boring (also known as the World’s Greatest Sin in story telling). But my blog is different. I can bore the hell out of you. But I wanted you to know that the science is real. So I go a little deeper here to show you the math behind the story.
Prometheus Blue is full of science, physics, astronomy, and rocketry. In this blog entry, I’m going to explain the physics and math behind the obliteration concept.
Could We Blow Up a Star?
What would that take?
To figure that out, we have to answer the following questions:
- Define “blowing up” a star. What’s it mean?
- How much mass does the star have?
- How much energy would we need to blow it up?
- What size of nuclear bomb would be required to deliver that much energy?
- How does physical placement of the bomb affect the result?
- So, could we do it?
Question 1 – What does it mean to “blow something up”? One definition that I like for blowing something up, particularly a cosmic body in space, is to violently separate its component parts such that they will not reconstitute without the further application of external forces. In other words, we are blasting the component particles far and wide such that their gravitational effects won’t bring it all back together again.
In the astro-physical meaning, I would say that blowing up a star means delivering enough energy to it to overcome the sum of its gravitational binding energy. Once this occurs, the star no longer exists in a gravitationally bound state. Simply put, it blows up and stays “blowed-up”.
Question 2 – How much mass does our target star have? Well our sun is pretty darn big. Its mass is about 2X1030 kilograms. That’s about 333,000 times the mass of the Earth. In Prometheus Blue, our menacing star (Blake’s Fragment in the book) is 87% the size of the sun, so it’s 1.73X1030 kilograms or 290,000 times the mass of the Earth. OK, so it’s big.
Question 3 – How much energy to blow up Blake’s Fragment? So now we get to calculate the gravitational binding energy of the star. We can go all the way back to Isaac Newton himself for this equation. Newton figured out that every physical body in the universe is bound by gravity and the properties that determine the magnitude of that gravity are the same everywhere. Those properties (and the units I will use) are its Mass (M) in kilograms, its Radius (R) in meters and its Shape. That’s it. But Newton was really even smarter than that. Hundreds of years ago, way back in 1687, Sir Isaac figured out equations that map the relationships among these variables. And he calculated a Universal Gravitational Constant – kind of a fudge factor – that would make it all work. Astoundingly, for a guy in the 17th century, he got this Constant right to a couple of decimal places. Here it is:
Gravitational Constant (G) = 6.674X10-11 m3/kg-sec2. Yeah, I know.
So the Gravitational Binding Energy g of a sphere is:
g = 3GM2/5R kg-m2/sec2 usually represented in joules.
But I’ve done the work for you. For a spherical body 87% the mass of the sun (per the book), that works out to 1.8 X 1040 joules. That’s how much energy we need to blow up a star. Well, this star anyway.
A joule is a pretty small bit of energy. It takes 360,000 of them to power a 100-watt light bulb for an hour. But come on, we’ve got 40 zeroes worth of joules here!
Question 4 – What size of nuclear bomb would it take to blow up our target star?
Here’s the fun part. A one megaton nuclear explosion releases about 4.2X1015 joules. Right now, the world’s stockpile is about 6,500 megatons. That’s a lot, right? We keep hearing how we’ve got enough nuclear explosive to destroy the world many times over. You’ve heard that one, right? Well, it turns out that it’s not really like that. Maybe we’ve got enough nuclear power for the radiation to kill us. I could believe that, I think. But to actually blow up the planet? Obliterate it? Nope. Not even close. Although I will concede that killing every living soul on the planet many times over is pretty bad. I’ll give you that one.
Anyway, with 6,500 megatons, we’ve got 2.7X1019 joules at our disposal. But we need 1040 joules. See where I’m going with this? We’re short by a factor of about 1020 times.
Let’s put that number into perspective.
Start with this: How much nuclear fuel does it take to deliver a one megaton nuclear blast? OK, skip ahead a few centuries and let’s ask Albert Einstein. Everyone knows his famous equation:
E = MC2. Energy = mass times the speed of light squared. So we know the energy we need, and we obviously know the speed of light. So the mass (M) of nuclear material we need to deliver our energy is M = E/C2. For a one megaton explosion, the mass we need works out to:
M (kg) = 4.2X1015 joules / 8.98X1016 = 0.047 kg. The units work out. Oh yeah. Trust me on this.
OK OK. Kg-m2-sec2/m2-sec2 = kg. There you go.
What this means is that 0.047 kilograms of matter will convert to a megaton of explosive power. Think of that. I pulled out the kitchen scale just now. A spoon from my utensil tray weighed exactly 48 grams. That was the SMALL spoon. The teaspoon. So a spoon-sized amount of matter converts to a million tonnes of TNT explosive. Yes way.
That’s definitely amazing, but it’s not the end of the story. Unfortunately (depending on your POV), the nuclear reaction isn’t nearly that efficient. Inside a nuclear explosion, we have most of the hydrogen, by far, in the nuclear reaction being converted to helium. What’s left over is about 0.712% of the mass. It is this mass that converts to blast energy. So dividing our 47 grams by 0.712%, and we’re left with 6.54 kilograms of fuel per megaton.
Unfortunately, it doesn’t end there. What I have calculated for you is the theoretical Einstein mass required to produce a megaton of explosive power. BUT, our nuclear technology isn’t nearly that efficient. Not even close. Certainly not yet.
In the middle part of the last century, a renowned nuclear physicist named Theodore (Ted) Taylor (not to be confused with the author Ted Taylor) postulated that there is a practical limit to the yield achievable from nuclear fuel. Ted Taylor was one of the most important nuclear physicists of the early-mid twentieth century. He pioneered small weapons technology and still holds the record for the most efficient nuclear device ever designed. There’s a pretty smart guy named Alex Wellerstein, a professor at the Stevens Institute of Technology in Hoboken and inventor of the insanely addictive Nuke Map (check out how big a blast it would take to wipe out your home town (or your mother-in-law’s home town). Professor Wellerstein has a really interesting blog. You should check it out. He talks about the Taylor Limit here.
So “Taylor’s Limit” is 6 kilotons of TNT equivalent explosion per kilogram of nuclear fuel. Put another way, that equates to 167 kilograms of fuel per megaton of explosive power. You can see this practical limit pretty clearly in the graph below:
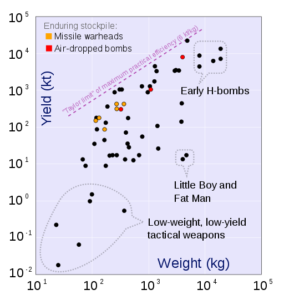
Here you can see the limit pretty starkly. 103 represents a megaton which gets us to 167 kg on the logarithmic X-axis. All those dots are actual nuclear explosive test results.
So there we have our bookends for this discussion: at the small end we have Einstein’s theoretical minimum of 6.54 kg per megaton and the Taylor Limit minimum 167 kg per megaton.
But Prometheus Blue is a science fiction thriller, routed in real science and physics. Combining those concepts, let’s say the nuclear geniuses of the future devise a bomb that approaches the Einstein limit of energy conversion. Now how big a bomb do we need to obliterate that star?
We’ve already established that we need 1.8X1040 joules. A one megaton nuclear bomb delivers 4.2X1015 joules. Simple division gives us the answer: we need 4.2X1025 megatons. What’s the combined power of Earth’s arsenal again? 6.5X103 megatons. We’re out by a factor of 1022. That’s all. No problemo. To give you a sense of how tiny an amount of nuclear power we have today compared to the gravitational binding energy of a sun-sized star, I did a little research.
Guess how many grains of sand there are in all the beaches of the world? Keep it in orders of magnitude. Meaning 10 followed by how many zeroes?
Well, it seems that researches at the University of Hawaii had too much time on their hands one day and they made an estimate. Looking at all the world’s beaches and estimating their length, width and depth and dividing that by the average size of a grain of sand, they came up with 7.5X1018 grains of sand. OK that’s just the beaches. Let’s gross that number up for the deserts. Let’s say (and I have absolutely no basis for this) that there are 10 times the number of grains of sand in the deserts as the beaches. Let’s gross the sand estimate up to 1020 grains.
What this means is that if Earth’s entire nuclear arsenal were represented by one single grain of sand, we would need to produce enough nuclear explosive force to Blake’s Fragment to fill every desert and every beach on Earth 100 times over!
Space is awesome.
How big a bomb is that? OK, 4.2X1025 megatons times Einstein’s 6.54 kg per megaton gives us a nuclear material weight of 2.82X1026 kilograms. Do you know how big that is?
Consider this: the mass of the entire planet Earth is estimated at 5.97X1024 kilograms. Uh-huh. You read that right. To blow up a Sun-sized star, we need more mass of nuclear material that the mass of our entire planet. 47 Earth’s actually.
So no, we can’t possibly deliver 47 Earth masses of nuclear explosive to a star several light-years away. Can’t be done. Sorry, science fiction ain’t gonna help ya here. Teleporting doesn’t count.
Do you actually think we’ll ever be able to blow up a star? See above.
Question 5 – How does bomb placement affect the explosive result?
Click on this video:
I describe this test in Prometheus Blue. This was an underground test at Sedan, Nevada on July 6, 1962. Believe it or not, the geniuses at Project Plowshare thought it might be a good idea to use low yield nuclear weapons as mining tools. I swear to gods I’m not making this up.
They buried a 104 kiloton nuclear bomb 194 meters below the desert and set it off. I think they really just wanted to blow shit up and watch the fun. It was fun all right. They moved about 11 million tons of dirt, launched a desert dome about 90 meters into the air, blew out a 390 meter wide X 100 meter deep crater and dispersed a nuclear fallout cloud about 5,000 meters into the atmo.
Dey blowed it up real good!
Of course any thoughts of mining that dead zone were abandoned instantly. But they achieved their prime objective, don’t you think?
But here’s the thing. In order to blow something up, to really obliterate it, you’ve got to place the charge near the center of the body you’re blowing up. Otherwise, you’re causing just surface damage. And believe it or not, that’s what Sedan represents. In real time, about 3 seconds after the dome began to rise, you can clearly see the venting of energy out of the dome. That’s wasted blast energy. Here’s a way to estimate the loss of efficiency of that bomb due just to its placement relatively near the surface.
I did the math. Again. Using the gravitational binding energy for bodies with the same density as Earth, a 104 kiloton charge, if placed in its center, would obliterate a sphere with a radius of 1.83 kilometers. That’s a volume of 2.6X1010 cubic meters. So that’s blowing up a sphere with the charge in its center. Now for Sedan. About that crater. A partly hemispherical crater 390 meters X 100 meters deep has a volume of about 9X106 cubic meters. That’s way less than our sphere. That’s a 0.035% efficiency. Or put another way, placing this bomb close to the surface resulted in a 99.965% loss of explosive energy to the atmosphere.
So yeah, placement is pretty darn important. That means we’ve got to deliver our little friend right into the heart of our target star.
How hard could it be?
Question 6 – So, could we blow up a star?
If you’ve been following along, I think you know the answer. Here’s some more star cud for you to chew on.
In my story Prometheus Blue, our star fragment – Blake’s Fragment – has a radius of 664,000 kilometers. She’s a fragment of a blue giant star, so she’s hot – maybe 50 to 100 million degrees in her core.
Now our fastest ever spacecraft will be the Parker Solar Probe. After getting several boosts from the Sun’s gravity, Parker is estimated to get up to about 665,000 kilometers an hour (that’s 185 kilometers per second). But in Prometheus Blue, we learn that our star fragment approached Barnard’s Star, just missed it and was flung off towards our solar system at 2,574 kilometers per second. So that dwarfs anything we can do yet.
Let’s say we’re going to deliver our bomb right into Blake’s Fragment – a chunk of blue star 87% the size of our Sun. Let’s say our bomb gets a gravity boost of triple speed as it approaches its target. So we’ve got a relative velocity of 3,128 kilometers per second. That means our bomb would still take 212 seconds to reach the core of Blake’s Fragment.
Did I mention that it’s 50 million degrees in there? So no, I don’t think any bomb is ever going to stay together for even second without vaporizing. Could it get to the core? Not a chance. Even if it could survive the journey, how would we detonate it so precisely that it went off at the center of the star? From 5 light-years away?
I’m not even going to talk about the crushing gravity at the center of the star.
So, could we blow up a star? Let me synthesize it for you.
In order to effectively blow up a star that is 87% of the size of the Sun, 5 light-years away and heading for Earth at 2,500 kilometers a second, we would need to launch a bomb that weighs 47 times more than the entire planet Earth, make it tough enough to withstand 50 million degrees and time the explosion to within a second from 5 light-years away.
Earth is screwed. We’re not stopping this thing.
But that won’t stop the politicians of this world from trying.
I’d like you to see how it all works out. I’ve written Prometheus Blue and its sequel Prometheus Red, depicting Humanity’s response to the knowledge that a planet killing event will occur in the far future. These two books complete the near future timeline of the Third Stone series. Future books will take us closer to the Event.
I’ll be seeking agent representation in late summer 2019 in my noble quest to get published. Follow my journey as an aspiring author as I navigate the canyons fo the New York publishing world!
If you’re interested to read how this all unfolds, let me know in the Comments below. I’d love to hear from you. And it might help me convince a publisher that the Prometheus story is worth reading.
Thanks for sticking it out!
To read the first few pages from my debut Science Fiction Thriller - Prometheus Blue - please click here (opens new window). I hope it intrigues you enough to want more. I'll be seeking agent representation to publish Prometheus Blue soon. The sequel - Prometheus Red - (excerpt here) will follow hot on her heels. If you leave a positive Comment, it will help me get published!

